【売上アップになるキャンペーン】串カツ田中のチンチロリンはすごい販促施策

前の記事では、串カツ田中のチンチロリンハイボールで得するかどうかの確率を出しました。

【確率を出してみた】串カツ田中のチンチロリンはやった方が得？

どのようなキャンペーンなのかについて紹介します。

ルールは簡単。サイコロを2つ振った時の目に応じて、お酒の価格が変わるというものです。

今回は、このキャンペーンがどれほどスゴイものなのかを、人間の心理にあてはめて考えてみます。

得するか否かの確率を出して気付きましたが、このキャンペーンはとても理にかなった素晴らしい販促プロモーションです。

そもそもデメリットがないキャンペーン

このキャンペーンですが、お客さんからしたら、損をしない仕組みになっています。なぜか？

実際にチンチロを振った時のことを考えてみましょう。

確率の記事でも紹介しましたが、サイコロの出る目を考えると得をする確率は50％。Wサイズで倍額になる確率は50％です。

仮に倍額になったとしても、2杯分を飲んでいるだけ。50％の確率で安く飲める上に、安くならなくても、2杯分を一気に頼んだことにしかならないのです。

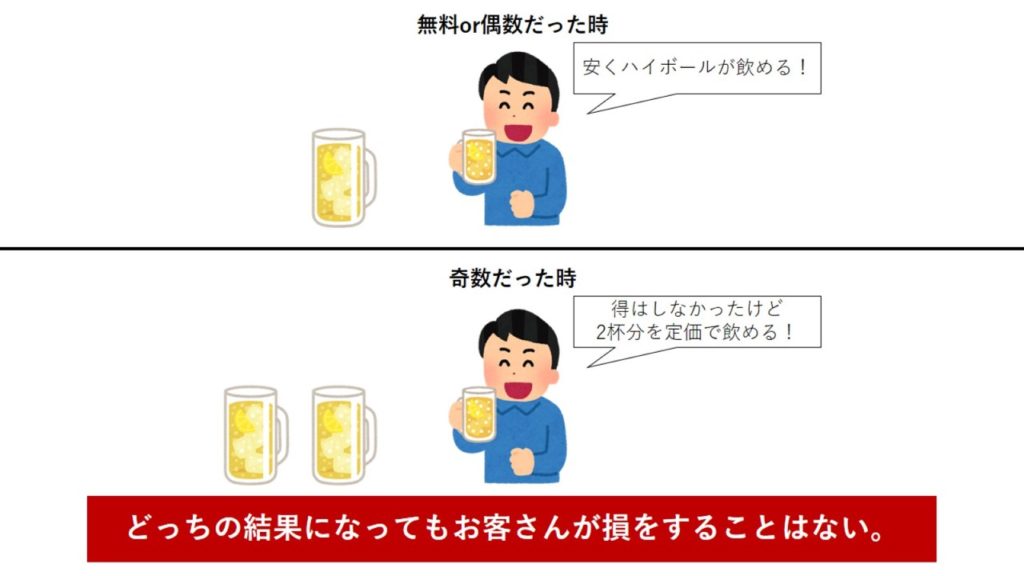
もし、これで奇数だったら価格が倍になるだけだったらどうでしょうか？　50％の確率で得をするが、50％の確率で損することになります。

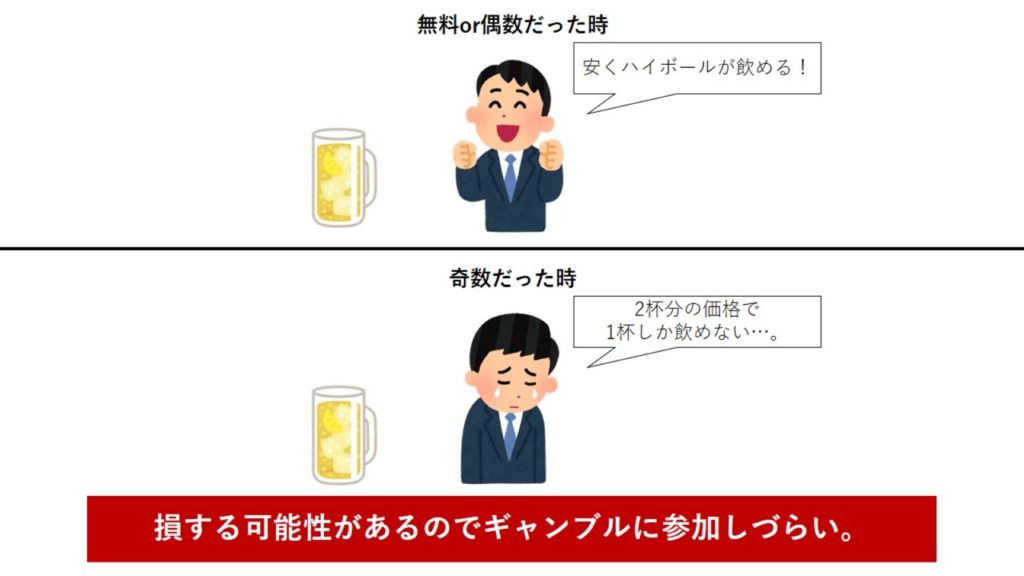
別の記事で紹介した通り、人間は損することに大きな抵抗を感じます。

【バチが当たる人とは？】悪いことをしたらバチが当たる論理的な理由

50％の確率で得をする（390円の飲み物が安くなる）けど、もう片方の50％になったとしても損はしない（2杯分を頼んだことになるだけ）。

このような設計だからこそ、お客さんは頼みやすいのです。

お店が儲かる仕組みが出来ている

先ほどはお客さんがチンチロリンを頼みやすい理由について説明しました。次はお店側の視点で考えてみます。

このチンチロリンハイボールというキャンペーンは、頼まれれば頼まれるほどお店が儲かる仕組みになっているのです。それはなぜか？

先ほども説明しましたが、チンチロをやった時に定価（390円）よりも安くなる確率は50％です。

もちろんチンチロを1回しかやらなければ、奇数が出ない限りお店の売上が大きくなることはありません。

ただ、複数人で飲みに行っている以上、チンチロを1回しかしない（お酒を1杯しか飲まない）ことはないでしょう。

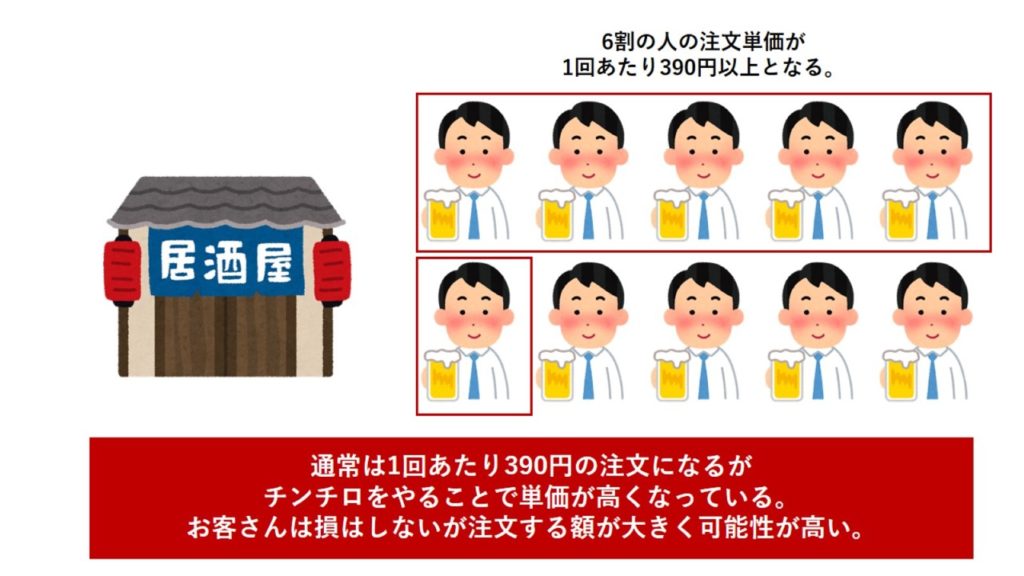
仮に2回やるとなった場合、以前の記事で紹介した通り、期待値が390円を超える確率は約60％。

期待値が定価よりも高い以上、1杯390円で何回も頼んでもらうより、チンチロで注文してもらう方が売上はアップするのです。

お客さんが頼む杯数をシレっと増やしている

ここまでの説明を聞くと、お客さんが損をしているという印象を持つかもしれません。でもそんなことはありません。お客さんも損はしていないです。

なぜなら、倍額のWサイズばかり出たとしても、1杯390円という価格には変わりないからです。

この施策のすごいところは、お客さんが飲むお酒の量を簡単に増やせることです。

お客さんからしたら【安く飲めるか？　一気に2杯頼むか？】の二択に見えます。価格での損がないので、リスクはありません。リターンしかないギャンブルとして積極的に参加しやすいでしょう。

でもお店側からしたら、50％の確率で2杯頼んでくれるというギャンブルです。勝てば、1回の注文金額（期待値）が高くなるという賭けをしています。

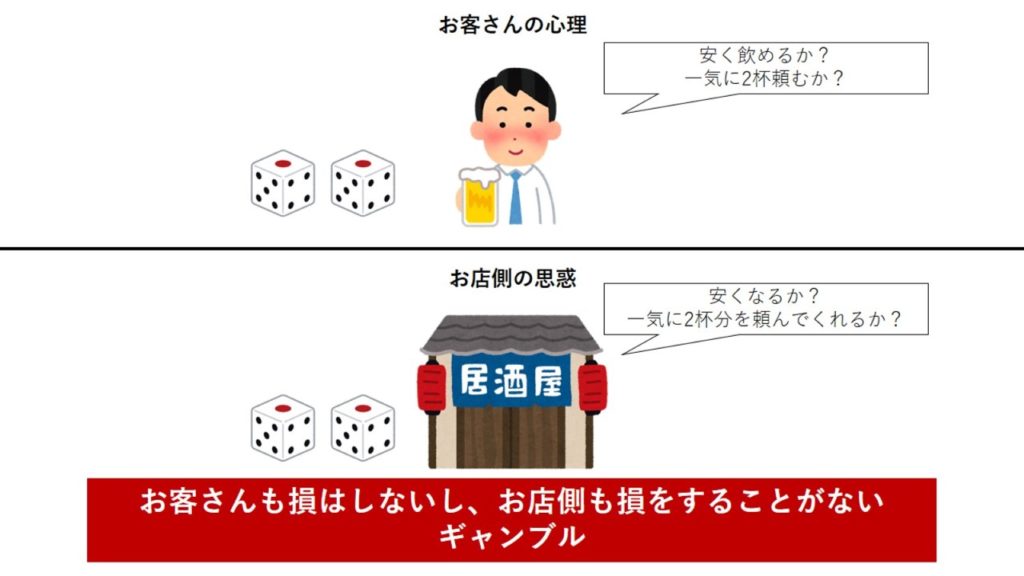
お客さんはリスクがないギャンブルをやってると思っています。しかし、知らず知らずのうちに、売上アップに貢献しているのです。

また、お客さんが2回チンチロに挑戦してくれたとした時、お店側の勝率は約60％。

お客さんからしてもリスクのないギャンブルですが、お店側はそれ以上にリスクがないギャンブルなのです。

まとめ

最後にこのキャンペーンの素晴らしさをまとめておきます。

間違いなく売上に寄与できる販促プロモーション。それなのにお客さんが損した気分にならない。むしろ得した気分になる施策なのです。みんなが気持ち良い気分になれる素晴らしいキャンペーンでした。

色々と応用ができそうな販促施策だなと思います。使える機会があれば、当てはめたいフレームワークですね！